Dalam mekanik kuantum, satu keadaan kuantum menerangkan objek pada skala yang sangat kecil, biasanya mewakili pergerakan zarah. Keadaan ini diwakili secara matematik oleh apa yang dipanggil sebagai fungsi gelombang. Keadaan tersebut hanyalah vektor yang merupakan elemen dalam ruang vektor, dikenali sebagai ruang Hilbert. Oleh itu, vektor adalah objek yang terkenal dalam aljabar linear, menjadikan kaedah aljabar linear sebagai alat yang kuat dalam mekanik kuantum yang menyatukan geometri dan aljabar secara lancar. Dengan pemahaman yang kukuh terhadap formulasi dan alat matematik mekanik kuantum, beberapa masalah canggih dalam sains dan teknologi kuantum boleh diubah kepada kaedah yang lebih mapan dan cekap dalam aljabar linear.

Salah satu contoh yang menjelaskan adalah transformasi masalah kompleksiti litar kuantum menjadi masalah geometri, yang kemudian boleh dikaji melalui lensa geometri Riemannian. Kompleksiti litar kuantum adalah isu yang mencabar dalam komputasi kuantum, memberi tumpuan kepada meningkatkan dan memajukan algoritma kuantum untuk mereka bentuk model litar kuantum yang cekap. Di sini, keadaan kuantum berubah menjadi qubit, pembawa maklumat kuantum, yang dioperasikan oleh pintu kuantum dalam algoritma khusus. Dalam usaha ini, qubit menggantikan bit klasik komputasi tradisional.

Kerja kami telah berjaya menyelami kompleksiti litar kuantum dalam kerangka geometri Riemannian, khususnya dalam konteks transformasi Fourier kuantum (QFT) tiga qubit (Rajah 1). Kami mengira dan mencadangkan Hamiltonian dan metrik Riemannian untuk QFT tiga qubit dan merumuskan persamaan geodesiknya dalam bentuk diferensial. Penyelesaian persamaan ini mencadangkan bahawa QFT yang cekap sebegini boleh direalisasikan.

Selain itu, kami menerangkan pintu kuantum dalam litar kuantum sebagai elemen kumpulan Lie SU(2) dalam representasi operator dan mencadangkan versi yang diperbaiki dari transformasi Fourier kuantum tiga qubit dalam SU(3) (Rajah 2). Frekuensi pemalar struktur bagi algebra Lie su(8) dalam asas Pauli dianalisis, mengesahkan bahawa semua litar kuantum pada dasarnya boleh dihasilkan menggunakan pintu satu qubit dan pintu CNOT. Ini memberi wawasan tentang hubungan antara model litar kuantum dan Algebra Lie.

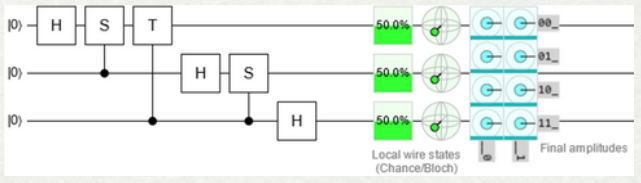Rajah 1: Litar kuantum transformasi Fourier tiga qubit dengan pintu Hadamard (H), S dan T.

Rajah 2: Representasi matriks untuk transformasi Fourier kuantum tiga qubit yang diperbaiki.

Rujukan

1. M.R. Dowling & M.A. Nielsen (2008). The geometry of quantum computation. Quantum Information & Computation, 8(10), 861–899.
2. H.E. Brandt (2009). Quantum computational geodesics. Journal of Modern Optics, 56(18-19), 2112–2117.
3. Chew Kang Ying, Nurisya Mohd Shah & Chan Kar Tim, (2022), Algebraic representation of three qubit quantum circuit problems, Malaysian Journal of Mathematical Sciences, 16(3):531-554.
   
   

Tentang Penulis
Dr. Nurisya Mohd Shah
Jabatan Fizik, Fakulti Sains, Universiti Putra Malaysia
Kepakaran: Fizik Kuantum, Fizik Matematik, Mekanik Kuantum Takkomutatif
Emel: risya@upm.edu.my

Tarikh Input: 18/03/2024 | Kemaskini: 18/03/2024 | harithdaniel